Survival analyse

Survival analyse wordt gebruikt voor data waarbij waarbij de tijd tot het optreden van een event van belang is. Met tijd wordt in deze bedoeld het aantal jaren, maanden of weken vanaf de start van de follow-up van een patient tot aan het optreden van een event. Het event kan overlijden zijn (vandaar de naam survival analyse), maar ook een relapse, herstel of een ander helder gedefinieerd eindpunt. In het algemeen wordt er bij survival analyse vanuit gegaan dat er maar 1 risico is en dat er 1 mogelijk event is. Bij meerdere risico's of meerdere herhalingen van een event zijn meer geavanceerde analyse technieken nodig zoals recurrent event survival analyse of competing risk survival analyse.

Bij het meten van tijd-tot-event data is vaak sprake van gecensureerde waarnemingen. Hierbij heb je iets aan informatie over de 'survival time' van een patient, maar weet je niet precies hoe lang de tijd-tot-event is. Censoring kan op drie manieren optreden:

• Een patient is gevolgd vanaf het begin van de study tot aan het eind van de 12 weekse studie periode. Op dat moment heeft de patient het event nog niet gekregen. We weten nu alleen dat de tijd-tot-event van deze persoon langer is dan 12 weken.
• Een patient trekt zich terug uit de studie na 6 weken, dus voor het eind van de studieperiode. Van deze persoon weten we alleen dat de tijd-tot event langer is dan 6 weken.
• Een patient start aan de studie maar raakt na het laatste contact op 8 weken 'lost to follow up'. Ook van deze patient weten we alleen dat de eventvrije periode langer is dan 8 weken.

Kaplan Meier analyse

Wanneer gebruik ik een Kaplan Meier analyse?

Om een schatting te maken van de survival curve wordt er vaak een Kaplan Meier analyse gebruikt. De Kaplan Meier analyse is een non-parametrische aanpak, waarbij de volgende aannames worden gebruikt:

• De prognose van patienten die vroeg of laat zijn geïncludeerd in de studie is gelijk.
• Patienten die de studie voortijdig verlaten of 'lost to follow up' raken hebben dezelfde prognose als patienten die tot aan het eind van de studie gevolgd zijn en geen event hebben gehad.
• Events gebeuren alleen op de waargenomen tijdstippen.

De Kaplan Meier procedure schat op ieder moment dat er bij een patient een event opgetreden is de survival functie (of cumulatieve proportie van 'survivors') op basis van het aantal personen dat op dat moment nog in de studie aanwezig is. Op deze manier wordt het resultaat minimaal beïnvloed door patienten die halverwege de rit gecensureerd raken. Een Kaplan-Meier analyse resulteert in een 'life table' en een survival curve. Bijvoorbeeld:

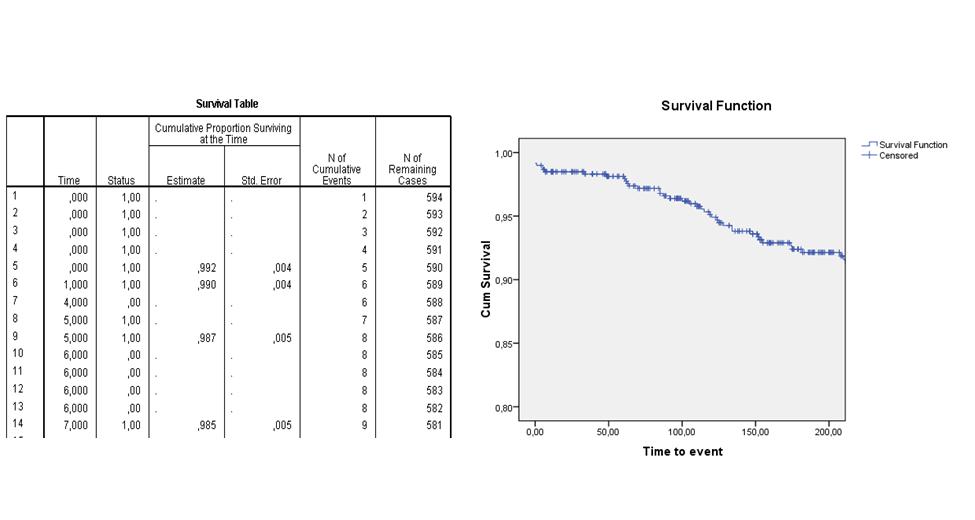
Hoe test ik of Kaplan Meier curves van elkaar verschillen?

Om te testen of de Kaplan Meier curves van 2 (of meer) groepen significant van elkaar verschillen, wordt vaak de log-rank test gebruikt. Deze test vergelijkt de geobserveerde verschillen tussen de survival curves met verschillen die puur op basis van toeval zouden kunnen ontstaan. In het volgende voorbeeld concluderen we bijvoorbeeld dat het verschil tussen treatment A en treatment B significant is:

Er zijn ook alternatieven voor de log rank test, namelijk:

• Wilcoxon test (in SPSS de Breslow test genoemd). Deze test weegt verschillen in het begin van de survival curves zwaarder dan verschillen aan het einde van de curves. De test is bijvoorbeeld geschikt om te bepalen of het effect van een behandeling op survival het sterkst is in de eerste fase en later minder effectief wordt.
• Tarone-Ware test. Deze test geeft net als de Wilcoxon test meer relatief meer gewicht aan verschillen op vroege momenten (maar minder uitgesproken dan de Wilcoxon test).

Waar vind ik de Kaplan Meier analyse in SPSS?

Je vindt de Kaplan Meier analyse in SPSS 16 onder Analyze -> Survival -> Kaplan-Meier.

Cox regressie

Wanneer gebruik ik een Cox proportional hazards model?

Wanneer er bij een survial analyse slechts een voorspellende factor onderzocht wordt, kan een Kaplan Meier analyse volstaan. Zijn er echter meerdere factoren die de overleving kunnen beinvloeden, dan is een uitgebreider model nodig. Een veel gebruikt model is Cox proportional hazards model. Hiermee kun je net als met andere multivariabele regressie modellen meerdere voorspellers tegelijk bestuderen. Voordeel van het Cox model boven een Kaplan Meier analyse is bovendien dat er naast de vraag "is er een effect" ook antwoord gegeven wordt op de vraag "hoe groot is het effect" van een bepaalde voorspeller. Het Cox model geeft de grootte van een effect weer met behulp van hazard ratio's (HR), waarbij een HR van 1 aangeeft dat er geen verschil is. Bijvoorbeeld: "During the 31-year follow-up, 87 women developed lung cancer. There was no association between hormone use and lung cancer (hazard ratio, 1.13; 95% CI, 0.73-1.73)."

Het Cox model maakt een belangrijke aanname, de proportional hazards assumptie. Deze zegt dat de HR's constant zijn in de tijd. Dit betekent dat het verschil is hazard veroorzaakt door verschillende waardes van een voorspeller gelijk blijft in de tijd.

Hoe test ik de proportional hazards assumptie binnen een Cox model?

Het verschil veroorzaakt door een bepaalde covariaat is onafhankelijk van de tijd. Bijvoorbeeld: het risicoverschil tussen man en vrouw is evengroot vlak na de procedure als na x jaar.

Er zijn meerdere manieren om de PH assumptie van een Cox model te testen:

• 1. grafisch

Als een variabele in het model voldoet aan de PH assumptie, dan zullen de geschatte overlevingscurves voor de strata binnen deze variabele parallel lopen. Je kunt hier naar kijken door in het cox model de variabele die je wilt onderzoeken niet meer als covariaat, maar als strata mee te geven en te vragen om log minus log survival plots. De resulterende syntax zal er ongeveer zo uitzien:

COXREG survt /STATUS=status(1) / STRATA=gender /METHOD=ENTER age TIMI etc. /PLOT LML /CRITERIA=PIN(.05) POUT(.10) ITERATE(20)

De twee resulterende lijnen moeten op het oog parallel lopen (zeker elkaar niet kruisen) om te voldoen aan de PH assumptie voor deze variabele (gender). Voor iedere variabele in het uiteindelijke model is een dergelijke plot nodig.

• 2. testen van (Schoenfeld) residuen

Er kan een officiele test gedaan worden mbv Schoenfeld residuen. Er is geen standaard functie hiervoor in SPSS. Ik kan eventueel wat code uit een boek copieren voor hoe dit in SPSS te berekenen. In Stata of R kan het wel direct.

• 3. Toevoegen van een tijdsafhankelijke variabele

Anticiperend op het mogelijk niet voldoen aan de PH assumptie kun je ook een time dependent cox draaien met daarin bijvoorbeeld de variabele GENDER*T. Als deze tijdsafhankelijke variabele significant bijdraagt aan het model, is er blijkbaar niet aan de PH assumptie voldaan.

Referenties

• Hosmer, D. W., and S. Lemeshow. 1999. Applied Survival Analysis. New York: John Wiley and Sons.
• Kleinbaum, D. G. 1996. Survival Analysis: A Self-Learning Text. New York: Springer-Verlag.
• Norusis, M. 2004. SPSS 13.0 Advanced Statistical Procedures Companion. Upper Saddle-River, N.J.: Prentice Hall, Inc..

Terug naar OVERZICHT voor een overzicht van alle statistische onderwerpen op deze wiki.

Terug naar KEUZE TOETS voor hulp bij het uitzoeken van een geschikte toets of analyse.