Herhaalde metingen: Difference between revisions
| Line 9: | Line 9: | ||
==Waarom kun je bij herhaalde metingen geen standaard regressie model gebruiken?== | ==Waarom kun je bij herhaalde metingen geen standaard regressie model gebruiken?== | ||
Bij een standaard regressie model wordt aangenomen dat alle metingen van elkaar | Bij een standaard regressie model wordt aangenomen dat alle metingen onafhankelijk van elkaar zijn. Bij herhaalde metingen is het waarschijnlijk dat twee metingen van dezelfde persoon meer op elkaar lijken dan twee metingen van verschillende personen. Als dat zo is, dan zijn de metingen binnen dezelfde persoon niet onafhankelijk. Als bij herhaalde metingen geen rekening wordt gehouden met deze afhankelijkheid, dan zijn i.h.a. de standaard fouten en de p-waardes (onterecht !) te klein. | ||
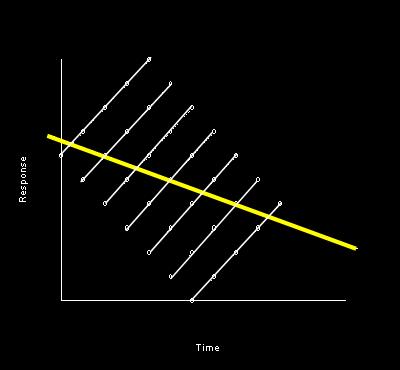
Bovendien kan de uitkomst van de regressie analyse volkomen fout zijn, zoals geillustreerd in het plaatje dat hieronder staat. In dit figuurtje worden de observaties van 6 personen getoond en elke persoon laat een duidelijk stijgende trend zien. Als de afhankelijkheid van de waarnemingen genegeerd wordt, dan is de best passende regressie lijn door de totale punten-wolk de gele dalende lijn en deze geeft geen correcte weergave van de trend per patient. | Bovendien kan de uitkomst van de regressie analyse volkomen fout zijn, zoals geillustreerd in het plaatje dat hieronder staat. In dit figuurtje worden de observaties van 6 personen getoond en elke persoon laat een duidelijk stijgende trend zien. Als de afhankelijkheid van de waarnemingen genegeerd wordt, dan is de best passende regressie lijn door de totale punten-wolk de gele dalende lijn en deze geeft geen correcte weergave van de trend per patient. | ||
Revision as of 12:29, 22 May 2009
Wat zijn herhaalde metingen?
Herhaalde metingen zijn meerdere metingen van dezelfde variabele bij dezelfde persoon/patient, proefdier, of algemeen geformuleerd, dezelfde observationele eenheid. Voorbeelden:
- tijd: als patienten herhaaldelijk in een follow-up periode worden gemeten (of: voor en na een behandeling);
- locatie: metingen op meerdere locaties in het lichaam van dezelfde persoon (linker en rechter oog, meerdere coupes in een biopt, meerdere slices in een MRI beeld);
- conditie: als dezelfde patient onder twee of meer verschillende condities (bijv. behandelingen) wordt gemeten;
- herhalingen tbv nauwkeurigheid: als een meting een grote variatie binnen een persoon heeft (of een grote meetfout) dan kan het zinvol zijn om een aantal aparte metingen te doen.
Waarom kun je bij herhaalde metingen geen standaard regressie model gebruiken?
Bij een standaard regressie model wordt aangenomen dat alle metingen onafhankelijk van elkaar zijn. Bij herhaalde metingen is het waarschijnlijk dat twee metingen van dezelfde persoon meer op elkaar lijken dan twee metingen van verschillende personen. Als dat zo is, dan zijn de metingen binnen dezelfde persoon niet onafhankelijk. Als bij herhaalde metingen geen rekening wordt gehouden met deze afhankelijkheid, dan zijn i.h.a. de standaard fouten en de p-waardes (onterecht !) te klein. Bovendien kan de uitkomst van de regressie analyse volkomen fout zijn, zoals geillustreerd in het plaatje dat hieronder staat. In dit figuurtje worden de observaties van 6 personen getoond en elke persoon laat een duidelijk stijgende trend zien. Als de afhankelijkheid van de waarnemingen genegeerd wordt, dan is de best passende regressie lijn door de totale punten-wolk de gele dalende lijn en deze geeft geen correcte weergave van de trend per patient.
Welke analyses zijn er mogelijk voor herhaalde metingen?
- Simpele methodes: meting van slechts een tijdpunt gebruiken, de verandering tussen twee meetpunten gebruiken, een samenvattende maat zoals het gemiddelde of de area under the curve
- Geavanceerde methodes: mixed models, repeated measurements ANOVA, Generalized Estimation Equations (GEE)
- kort voor en nadelen van deze methodes
De simpele methodes gebruiken maar een deel van de verzamelde informatie en dat levert vaak minder onderscheidingsvermogen (power) op. repeated measurements ANOVA is een specifieke variant van mixed-models, maar is alleen beschikbaar voor continue normaal verdeelde afhankelijke variabelen, die op vaste en dezelfde tijdstippen zijn gemeten in alle patienten. Mixed-models en GEE-modellen zijn wat lastiger te specificeren, maar zijn flexibeler en zijn beschikbaar voor zowel continue normaal verdeelde afhankelijke variabelen, maar ook voor bijv dichotome afhankelijke variabelen.
area under the curve
Wat is een area under the curve en wanneer kun je die gebruiken?
Hoe bereken ik met SPSS een area under the curve bij herhaalde metingen?
Ik wil graag van een bepaalde meting in de tijd, op verschillende tijdstippen gemeten, de 'area under the curve' bepalen. Ik kom er met SPSS niet uit. Ik moet er nl een stuk of 300 bepalen... heeft u nog een advies?
Je kunt de volgende syntax gebruiken, deze rekent per patient een area under the curve uit. Bovenaan het document staat beschreven hoe je de variabelen in SPSS moet hebben staan.
mixed models
Waarin verschilt een mixed model van een gewoon regressiemodel?
Correlaties/covarianties tussen meetpunten worden meegemodelleerd.
Hier eventueel formule
Hoe modelleer ik de covariantiestructuur van mijn mixed model?
Twee opties: 1. direct de covariantie structuur specificeren 2. random effects specificeren
Waar vind ik linear mixed models in SPSS?
Je vindt de linear mixed models in SPSS 16 onder Analyze->Mixed models->Linear. In SPSS 16 is er alleen nog een mixed model beschikbaar voor lineaire uitkomsten. In andere pakketten zoals R en SAS zijn er ook mixed modellen beschikbaar voor bijvoorbeeld dichotome uitkomstmaten.
Voorbeeld: hoe analyseer ik met een mixed model een effect in de tijd?
Ik onderzoek een groep patienten die een operatie hebben ondergaan. We zijn geinteresseerd in de pijnscore (VAS) op verschillende tijdsmomenten na de operatie. De verwachting is (uiteraard) dat de pijn direct na de operatie heviger is dan bijv. 3 mnd daarna (dit klopt ook als je de data in een barplot zet). In eerste instantie heb ik de ANOVA for repeated measures gebruikt om te analyseren of de pijn significant verandert in de tijd. Maar, omdat ik een aantal missing data heb, heb ik ook geprobeerd een mixed models analyse (hier mijn syntax) te doen. Mijn vragen hierover:
1. Heb ik de juiste covariance structure gebruikt? (nl. AR1)
2. Ik heb 'tijd' als fixed effect genomen omdat de afname van de VAS op specifieke tijdsmomenten gebeurde, klopt dat?
3. Hoe geef de resultaten van deze mixed analyse weer?
1. Of AR(1) de beste is is niet zo te zeggen, dat hangt af van de correlatie tussen de tijdsmomenten in jouw data. Je kunt bijvoorbeeld alle mogelijke structuren draaien en dan degene met de kleinste AIC te kiezen (smaller is better zoals er ook onder staat).
2. Tijd is hier inderdaad een fixed variable, want je wilt hier de hypothese toetsen of er een verandering in de tijd is.
3. In de output vind je onder "fixed effects" een B (beta) die aangeeft wat het effect is per tijdspunt (tov het startpunt) en een bijbehorende p-waarde. Dit is de toets die je waarschijnlijk wilt rapporteren. Onder het kopje "mean estimates" vind je de schatting van het model voor de gemiddelde VAS waarde op ieder tijdpunt. Deze mean estimates zijn voor een lezer makkelijker te interpreteren dan de betas.
repeated measurements ANOVA
Wanneer kan ik een repeated measurements ANOVA gebruiken?
- geen / niet te veel missings
- vaste covariantie structuur
Waar vind ik de repeated measurements ANOVA in SPSS?
Je vindt de repeated measurements ANOVA in SPSS 16 onder Analyze->General Linear Model->Repeated measures.
Referenties
Terug naar OVERZICHT voor een overzicht van alle statistische onderwerpen op deze wiki.
Terug naar KEUZE TOETS voor hulp bij het uitzoeken van een geschikte toets of analyse.